백인감자
[인공지능] Learning from Examples - 1 본문
이슈사항 : validation set 이라는 것은 test set 하기 전에 예측해보는 그런 느낌이다, overfitting 을 막기 위해 사용된다.
Test set 은 가장 마지막에 사용하는거라서 학습용으로 쓰면 안됨. 그리고 미지의 데이터 전체를 잘 나타내야함
validation set 은 test set 을 잘 표현할 수 있어야한다.
Supervised Learning (지도 학습)
input, output(label) 의 쌍들에 대한 정보를 알고 있는 상태에서 학습시킨다.
input 에 대한 정보만 알고 있는 상태에서 학습 시키는 것을 Unsupervised Learning (자율 학습) 이라고 한다.
용어
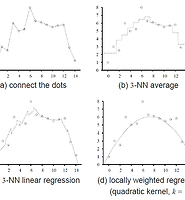
regression : 회귀 , 두 변수 x, y 의 관계를 표현하는 적합한 식을 의미한다.
Ockham's razor : 오컴의 면도날, 같은 현상을 설명하는 가설들이 있으면 가장 간단한 가설을 선호한다는 뜻이다.
이 강의자료에서 주로 물어본 내용 : decision tree 만들기
n개의 Boolean attribute 를 가지고 있다면 2^(2^n) 개의 distinct decision tree를 가질 수 있다.
decision tree 를 작성할 때 어떤 attribute 를 기준으로 하느냐에 따라서 classification 이 달라진다.
이상적인 attribute 를 사용했을 경우 all positive or all negative 처럼 극단적으로 분류될 것이다.(엔트로피가 낮다.)
Information gain이란 특정 속성을 기준으로 example들을 구분하게될 때 감소되는 entropy의 양을 의미
엔트로피는 아래와 같은 공식으로 계산할 수 있다. c는 target 속성이 가지는 값의 종류이다.(ex. target 이 true, false 같은 진리값만 가진다면 c=2 이다.)
예를 들어 positive 와 negative 의 개수가 동일하게 나온다면 Entropy 는 1 이 되고
전부 positive 이거나 전부 negative 이면 Entropy 는 0 이 된다.
어떤 example E 를 특정 attribute 를 기준으로 split 할 때 attribute 가 예를들어 날씨라면 {맑음, 흐림, 비} 로 3개의 값이 있다고 할 때
엔트로피 계산을 수식으로 표현하면 다음과 같다. p= positive , n= negative 를 의미한다.
i=1부터 3까지 반복된다.
Information gain 의 경우 attribute 의 값이 예를 들어 주민번호나 학번같이 example 들이 서로 다른 값을 가지거나 음식의 가격같이 다양한 값을 가지는 Multivalued Attribute 인 경우 information gain 이 매우 높게 나와서 좋은 attribute 를 선택할 때 잘못된 결과를 초래할 수 있다. 그럴 때를 위해 gain ratio 를 사용한다.
split point 를 선택할 때는 모든 가능한 split point 에 대해서 Entropy 를 계산해본 후 Entropy 값이 가장 작게 나오는 경우를 split point 로 선택해야 한다. 다른 attribute 와 비교할 때 gain ratio 값으로 비교를 하면 된다.
decision tree에 대한 예제를 보자. 아래의 표에 대응하는 information gain 을 통해 minimum decision tree를 그리는 것이 목표다.
Windy 에서 Weak(==false) , Strong(==true) 로 생각하고 계산하면 된다.(자료의 표기 오류 때문.)
테니스를 할 지에 대한 decision tree 를 그리는 것이다. Day 와 PlayTennis 를 제외한 나머지가 attribute 이다.
1. 우선 root node 에 어떤 attribute 가 와야하는지에 대해서 계산을 해야한다.
모든 속성에 대해서 엔트로피를 계산하여 가장 낮은 엔트로피를 가지는 attribute 를 선택하면 된다.
+는 Yes 의 수 , -는 No 의 수 이다.
우선 Outlook 에 대해서 계산을 해보면
Sunny [2+,3-]
Overcast [4+,0-]
Rain [3+,2-]
와 같은 형태로 표현할 수 있다. 이 값들을 통해 엔트로피 계산을 하면 아래와 같이 나온다. 나머지 attribute 에 대한 계산도 포함되어있다.
outlook, temperature 같은 경우 속성값이 3종류 이므로 Multivalued Attribute 이다.
4개의 속성 중 outlook 의 엔트로피가 가장 낮기 때문에 root node 는 outlook 이 된다.
2. outlook(root node) 은 3가지의 branch 가 있으므로 각 branch 에 올 수 있는 attribute 를 순서대로 구해본다.
2-1. 우선 sunny 라는 branch 에 대해서 해보자.
yes,no 에 대한 분류만 해놓은 상태에서 보면 Humidity 가 all no, all yes 로 나뉜 것을 확인할 수 있다. 즉, 엔트로피가 0이므로
따로 계산할 필요 없이 Humidity 가 최적이라는 것을 확인할 수 있다.
2-2. overcast 라는 branch 에 대해 계산해보면 다음과 같다.
모든 attribute 의 엔트로피가 0 이고 전부 yes 이기 때문에 yes 를 적어주면 된다.(leaf node)
2-3. rainy 라는 branch 에 대해서도 계산해보면 다음과 같다.
windy 라는 attribute 의 엔트로피가 0이기 때문에 windy 를 선택한다.
다음 level 에서도 같은 방법을 적용하여 계산을 하면 decision tree의 모양은 아래와 같다.
temperature 라는 attribute 는 decision tree에 사용되지 않으므로 불필요한 속성이라고 볼 수 있다.
추가적으로 root level 에서의 각 attribute에 대해서 gain ratio 을 구한다면 다음과 같다.
분류전의 전체 엔트로피 = 0.9403
decision tree 구하는 과정에서 각 속성의 root level 에서의 엔트로피는 위에서 계산되었으므로 그대로 이용하면 된다.
gain ratio(== information gain) 이 가장 높은 outlook 이 root node 가 된다는 것을 다시 한 번 확인 할 수 있다.
outlook 은 전체 14개가 5,4,5 로 나뉘기 때문에 splitinfo를 아래와 같이 작성하는것이고 나머지도 마찬가지이다.
training set 이 클수록 확률이 높아지지만 좋은 것만은 아니다. redundant 한 값들이 많아지기 때문이다.
이를 해결하기 위해 Pruning 을 수행해야한다.
이러한 방법의 예시가 카이 제곱 pruning 이다.
모델의 평가와 선택
미래의 데이터에 가장 잘 맞는 모델 h를 학습한다.
모델을 선택하고 평가할 때 test-set 의 성능을 사용하면 안된다.
cross-validation 을 실시하라.
cross-validation(교차검증) :기존 training set 의 일부를 validation set 으로 설정한다. validation set 의 error rate 을 통해서 overfitting 을 감지하고 예방할 수 있다.
k-fold cross validation : data set 를 k개의 동등한 조각으로 나눈다. 1조각을 validation set 으로 하고 나머지 k-1 조각을 training set으로 사용한다. k번을 반복하면서 서로 다른 조각들이 한 번씩 validation set 으로 설정되고 이들의 평균값을 통해 error rate을 확인한다. 모든 데이터가 validation set 으로 사용이 되었기 때문에 좀 더 정확하다고 볼 수 있다.
LOOCV(Leave-one-out cross-validation) : k-fold cross validation에서 k를 data set 의 전체 개수인 n (k=n) 으로 하는 방식.
모든 데이터에 대해 다 평가하기 때문에 계산 비용이 많이 든다.
to avoid peeking in doing model selection
test-set 은 건들지 않는다.
divide the available data into a training set and a validation set to measure performance on unseen data as a way of selecting a good hypothesis
좋은 모델을 선택하는 방법으로 보이지 않는 데이터의 성능을 측정하기 위해 사용 가능한 데이터를 training set 과 validation set으로 나눈다. --> 기존 training set 을 training set 과 validation set 으로 나눈다.
좋은 모델은 validation set error(=cross validation error) 가 가장 낮은 것이다.아래 그림은 k-fold cross-validation 을 k=10 으로 설정하고 수행한 것이다. Tree size 가 7 일 때가 최적의 모델인데 7보다 더 커지게되면 validation set error 가 증가하는 모습을 볼 수 있는데 이것은 overfitting(과적합) 되고 있다는 뜻이다. cross validatioin 방식을 통해서 overfitting 을 막을 수 있게 된다.
아래 그림을 보면서 의문이 생기는 것은 왜 항상 Training Set Error 가 Validation Set Error 보다 낮은 값을 가지는지이다.
--> Traning set 의 개수가 Validation set 보다 많기 때문에 일반적으로 error rate 이 낮다고 본다.(예외는 존재할 수 있다.)
'인공지능' 카테고리의 다른 글
| cifar10 모델 평가하기 & 텐서보드로 확인 (0) | 2017.08.21 |
|---|---|
| [인공지능] Learning from Examples - 3 (0) | 2017.05.31 |
| [인공지능] Tensorflow 환경구축 for Windows (0) | 2017.04.30 |
| [Python2.7] matplotlib +numpy +scipy 환경구축 (Windows7 32bit) (0) | 2017.03.26 |
| [인공지능] Uninformed Search Strategies (0) | 2017.03.10 |